put Methoddelete Methodget Methodmy_dict={'Dave' : '001' , 'Ava': '002' , 'Joe': '003'}
print(my_dict)
type(my_dict)new_dict=dict()
print(new_dict)
type(new_dict)new_dict=dict(Dave = '001' , Ava= '002' , Joe= '003')
print(new_dict)
type(new_dict)emp_details = {'Employee': {'Dave': {'ID': '001',
'Salary': 2000,
'Designation':'Python Developer'},
'Ava': {'ID':'002',
'Salary': 2300,
'Designation': 'Java Developer'},
'Joe': {'ID': '003',
'Salary': 1843,
'Designation': 'Hadoop Developer'}}}my_dict={'Dave' : '001' , 'Ava': '002' , 'Joe': '003'}
my_dict\['Dave'\]my_dict={'Dave' : '001' , 'Ava': '002' , 'Joe': '003'}
print(my_dict.keys())
print(my_dict.values())
print(my_dict.get('Dave'))my_dict={'Dave' : '001' , 'Ava': '002' , 'Joe': '003'}
print("All keys")
for x in my_dict:
print(x) #prints the keys
print("All values")
for x in my_dict.values():
print(x) #prints values
print("All keys and values")
for x,y in my_dict.items():
print(x, ":" , y) #prints keys and valuesmy_dict={'Dave' : '001' , 'Ava': '002' , 'Joe': '003'}
my_dict\['Dave'\] = '004' #Updating the value of Dave
my_dict\['Chris'\] = '005' #adding a key-value pair
print(my_dict)my_dict={'Dave': '004', 'Ava': '002', 'Joe': '003', 'Chris': '005'}
del my_dict\['Dave'\] #removes key-value pair of 'Dave'
my_dict.pop('Ava') #removes the value of 'Ava'
my_dict.popitem() #removes the last inserted item
print(my_dict)import pandas as pd
emp_details = {'Employee': {'Dave': {'ID': '001',
'Salary': 2000,
'Designation':'Python Developer'},
'Ava': {'ID':'002',
'Salary': 2300,
'Designation': 'Java Developer'},
'Joe': {'ID': '003',
'Salary': 1843,
'Designation': 'Hadoop Developer'}}}
df=pd.DataFrame(emp_details\['Employee'\])
print(df)L -> 01001100
A -> 01000001
M -> 01001101
B -> 01000010
D -> 01000100
A -> 01000001bytes_representation = "hello".encode()
for byte in bytes_representation:
print(byte)
### Print Output
### 104
### 101
### 108
### 108
### 111bytes_representation = "hello".encode()
sum = 0
for byte in bytes_representation:
sum += byte
print(sum)
### Print Output
### 532def my_hashing_func(str):
bytes_representation = str.encode()
sum = 0
for byte in bytes_representation:
sum += byte
return sumdef my_hashing_func(str, table_size):
bytes_representation = str.encode()
sum = 0
for byte in bytes_representation:
sum += byte
return sum % table_sizeclass HashTable:
"""
A hash table with `capacity` buckets
that accepts string keys
"""
def __init__(self, capacity):
self.capacity = capacity # Number of buckets in the hash table
self.storage = [None] * capacity
self.item_count = 0
def get_num_slots(self):
"""
Return the length of the list you're using to hold the hash table data. (Not the number of items stored in the hash table,
but the number of slots in the main list.)
One of the tests relies on this.
"""
return len(self.storage)
def djb2(self, key):
"""
DJB2 hash, 32-bit
"""
# Cast the key to a string and get bytes
str_key = str(key).encode()
# Start from an arbitrary large prime
hash_value = 5381
# Bit-shift and sum value for each character
for b in str_key:
hash_value = ((hash_value << 5) + hash_value) + b
hash_value &= 0xffffffff # DJB2 is a 32-bit hash, only keep 32 bits
return hash_value
def hash_index(self, key):
"""
Take an arbitrary key and return a valid integer index within the hash table's storage capacity.
"""
return self.djb2(key) % self.capacity
def put(self, key, value):
"""
Store the value with the given key.
"""
def delete(self, key):
"""
Remove the value stored with the given key.
Print a warning if the key is not found.
"""
def get(self, key):
"""
Retrieve the value stored with the given key.
Returns None if the key is not found.
"""def put(self, key, value):
"""
Store the value with the given key.
"""
index = self.hash_index(key)def put(self, key, value):
"""
Store the value with the given key.
"""
index = self.hash_index(key)
self.storage[index] = value
returndef delete(self, key):
"""
Remove the value stored with the given key.
"""
index = self.hash_index(key)def delete(self, key):
"""
Remove the value stored with the given key.
"""
index = self.hash_index(key)
self.storage[index] = Nonedef get(self, key):
"""
Retrieve the value stored with the given key.
Returns None if the key is not found.
"""
index = self.hash_index(key)def get(self, key):
"""
Retrieve the value stored with the given key.
Returns None if the key is not found.
"""
index = self.hash_index(key)
return self.storage[index]class HashTableEntry:
"""
Hash table key/value pair to go in our collision chain
"""
def __init__(self, key, value):
self.key = key
self.value = value
# Hash table can't have fewer than this many slots
MIN_CAPACITY = 8
class HashTable:
"""
A hash table with `capacity` buckets
that accepts string keys
Implement this.
"""
def __init__(self, capacity):
self.capacity = capacity # Number of buckets in the hash table
self.storage = []
for _ in range(capacity): # Initialize with empty lists
self.storage.append([])
self.item_count = 0
def get_num_slots(self):
"""
Return the length of the list you're using to hold the hash table data. (Not the number of items stored in the hash table,
but the number of slots in the main list.)
One of the tests relies on this.
Implement this.
"""
# Your code here
def get_load_factor(self):
"""
Return the load factor for this hash table.
Implement this.
"""
return len(self.storage)
def djb2(self, key):
"""
DJB2 hash, 32-bit
Implement this, and/or FNV-1.
"""
str_key = str(key).encode()
hash = FNV_offset_basis_64
for b in str_key:
hash *= FNV_prime_64
hash ^= b
hash &= 0xffffffffffffffff # 64-bit hash
return hash
def hash_index(self, key):
"""
Take an arbitrary key and return a valid integer index between within the hash table's storage capacity.
"""
return self.djb2(key) % self.capacity
def put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
# Your code here
def delete(self, key):
"""
Remove the value stored with the given key.
Print a warning if the key is not found.
Implement this.
"""
# Your code here
def get(self, key):
"""
Retrieve the value stored with the given key.
Returns None if the key is not found.
Implement this.
"""
# Your code here def put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
# Your code here def put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
chain = self.storage[index] def put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
chain = self.storage[index]
existing_entry = None
for current_entry in chain:
if current_entry.key == key:
exiting_entry = current_entry
break def put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
chain = self.storage[index]
existing_entry = None
for current_entry in chain:
if current_entry.key == key:
existing_entry = current_entry
break
if existing_entry is not None:
existing_entry.value = value
else:
new_entry = HashTableEntry(key, value)
chain.append(new_entry)class HashTableEntry:
"""
Linked List hash table key/value pair
"""
def __init__(self, key, value):
self.key = key
self.value = value
self.next = None
# Hash table can't have fewer than this many slots
MIN_CAPACITY = 8
class HashTable:
"""
A hash table with `capacity` buckets
that accepts string keys
Implement this.
"""
def __init__(self, capacity):
self.capacity = capacity # Number of buckets in the hash table
self.storage = [None] * capacity
self.item_count = 0
def get_num_slots(self):
"""
Return the length of the list you're using to hold the hash
table data. (Not the number of items stored in the hash table,
but the number of slots in the main list.)
One of the tests relies on this.
Implement this.
"""
# Your code here
def get_load_factor(self):
"""
Return the load factor for this hash table.
Implement this.
"""
return self.item_count / self.capacity
def resize(self, new_capacity):
"""
Changes the capacity of the hash table and
rehashes all key/value pairs.
Implement this.
"""
old_storage = self.storage
self.capacity = new_capacity
self.storage = [None] * self.capacity
current_entry = None
# Save this because put adds to it, and we don't want that.
# It might be less hackish to pass a flag to put indicating that
# we're in a resize and don't want to modify item count.
old_item_count = self.item_count
for bucket_item in old_storage:
current_entry = bucket_item
while current_entry is not None:
self.put(current_entry.key, current_entry.value)
current_entry = current_entry.next
# Restore this to the correct number
self.item_count = old_item_count
def djb2(self, key):
"""
DJB2 hash, 32-bit
Implement this, and/or FNV-1.
"""
str_key = str(key).encode()
hash = FNV_offset_basis_64
for b in str_key:
hash *= FNV_prime_64
hash ^= b
hash &= 0xffffffffffffffff # 64-bit hash
return hash
def hash_index(self, key):
"""
Take an arbitrary key and return a valid integer index
within the hash table's storage capacity.
"""
return self.djb2(key) % self.capacity
def put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
while current_entry is not None and current_entry.key != key:
current_entry = current_entry.next
if current_entry is not None:
current_entry.value = value
else:
new_entry = HashTableEntry(key, value)
new_entry.next = self.storage[index]
self.storage[index] = new_entry
def delete(self, key):
"""
Remove the value stored with the given key.
Print a warning if the key is not found.
Implement this.
"""
# Your code here
def get(self, key):
"""
Retrieve the value stored with the given key.
Returns None if the key is not found.
Implement this.
"""
# Your code heredef put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
while current_entry is not None and current_entry.key != key:
current_entry = current_entry.next
if current_entry is not None:
current_entry.value = value
else:
new_entry = HashTableEntry(key, value)
new_entry.next = self.storage[index]
self.storage[index] = new_entrydef put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
while current_entry is not None and current_entry.key != key:
current_entry = current_entry.next
if current_entry is not None:
current_entry.value = value
else:
new_entry = HashTableEntry(key, value)
new_entry.next = self.storage[index]
self.storage[index] = new_entry
self.item_count += 1def put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
while current_entry is not None and current_entry.key != key:
current_entry = current_entry.next
if current_entry is not None:
current_entry.value = value
else:
new_entry = HashTableEntry(key, value)
new_entry.next = self.storage[index]
self.storage[index] = new_entry
self.item_count += 1
if self.get_load_factor() > 0.7:
self.resize(self.capacity * 2)class HashTableEntry:
"""
Linked List hash table key/value pair
"""
def __init__(self, key, value):
self.key = key
self.value = value
self.next = None
# Hash table can't have fewer than this many slots
MIN_CAPACITY = 8
class HashTable:
"""
A hash table with `capacity` buckets
that accepts string keys
Implement this.
"""
def __init__(self, capacity):
self.capacity = capacity # Number of buckets in the hash table
self.storage = [None] * capacity
self.item_count = 0
def get_num_slots(self):
"""
Return the length of the list you're using to hold the hash
table data. (Not the number of items stored in the hash table,
but the number of slots in the main list.)
One of the tests relies on this.
Implement this.
"""
# Your code here
def get_load_factor(self):
"""
Return the load factor for this hash table.
Implement this.
"""
return self.item_count / self.capacity
def resize(self, new_capacity):
"""
Changes the capacity of the hash table and
rehashes all key/value pairs.
Implement this.
"""
old_storage = self.storage
self.capacity = new_capacity
self.storage = [None] * self.capacity
current_entry = None
# Save this because put adds to it, and we don't want that.
# It might be less hackish to pass a flag to put indicating that
# we're in a resize and don't want to modify item count.
old_item_count = self.item_count
for bucket_item in old_storage:
current_entry = bucket_item
while current_entry is not None:
self.put(current_entry.key, current_entry.value)
current_entry = current_entry.next
# Restore this to the correct number
self.item_count = old_item_count
def djb2(self, key):
"""
DJB2 hash, 32-bit
Implement this, and/or FNV-1.
"""
str_key = str(key).encode()
hash = FNV_offset_basis_64
for b in str_key:
hash *= FNV_prime_64
hash ^= b
hash &= 0xffffffffffffffff # 64-bit hash
return hash
def hash_index(self, key):
"""
Take an arbitrary key and return a valid integer index
within the hash table's storage capacity.
"""
return self.djb2(key) % self.capacity
def put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
while current_entry is not None and current_entry.key != key:
current_entry = current_entry.next
if current_entry is not None:
current_entry.value = value
else:
new_entry = HashTableEntry(key, value)
new_entry.next = self.storage[index]
self.storage[index] = new_entry
def delete(self, key):
"""
Remove the value stored with the given key.
Print a warning if the key is not found.
Implement this.
"""
# Your code here
def get(self, key):
"""
Retrieve the value stored with the given key.
Returns None if the key is not found.
Implement this.
"""
# Your code heredef put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
while current_entry is not None and current_entry.key != key:
current_entry = current_entry.next
if current_entry is not None:
current_entry.value = value
else:
new_entry = HashTableEntry(key, value)
new_entry.next = self.storage[index]
self.storage[index] = new_entrydef put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
while current_entry is not None and current_entry.key != key:
current_entry = current_entry.next
if current_entry is not None:
current_entry.value = value
else:
new_entry = HashTableEntry(key, value)
new_entry.next = self.storage[index]
self.storage[index] = new_entry
self.item_count += 1def put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
while current_entry is not None and current_entry.key != key:
current_entry = current_entry.next
if current_entry is not None:
current_entry.value = value
else:
new_entry = HashTableEntry(key, value)
new_entry.next = self.storage[index]
self.storage[index] = new_entry
self.item_count += 1
if self.get_load_factor() > 0.7:
self.resize(self.capacity * 2)
def csMaxNumberOfLambdas(text):
sub_string = "lambda"
lambda_count = {"l": 0, "a": 0, "m": 0, "b": 0, "d": 0, "a": 0}
counts = []
for letter in text:
if letter in lambda_count:
lambda_count[letter] += 1
for key, value in lambda_count.items():
counts.append(value)
return min(counts)




Searching & Recursion
def linear_search(arr, target):
# loop through each item in the input array
for idx in range(len(arr)):
# check if the item at the current index is equal to the target
if arr[idx] == target:
# return the current index as the match
return idx
# if we were able to loop through the entire array, the target is not present
return -1def function():
x = 10
function()>>> function()
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<stdin>", line 3, in function
File "<stdin>", line 3, in function
File "<stdin>", line 3, in function
[Previous line repeated 996 more times]
RecursionError: maximum recursion depth exceeded>>> from sys import getrecursionlimit
>>> getrecursionlimit()
1000>>> from sys import setrecursionlimit
>>> setrecursionlimit(2000)
>>> getrecursionlimit()
2000>>> def countdown(n):
... print(n)
... if n == 0:
... return # Terminate recursion
... else:
... countdown(n - 1) # Recursive call
...
>>> countdown(5)
5
4
3
2
1
0def countdown(n):
print(n)
if n > 0:
countdown(n - 1)>>> def countdown(n):
... while n >= 0:
... print(n)
... n -= 1
...
>>> countdown(5)
5
4
3
2
1
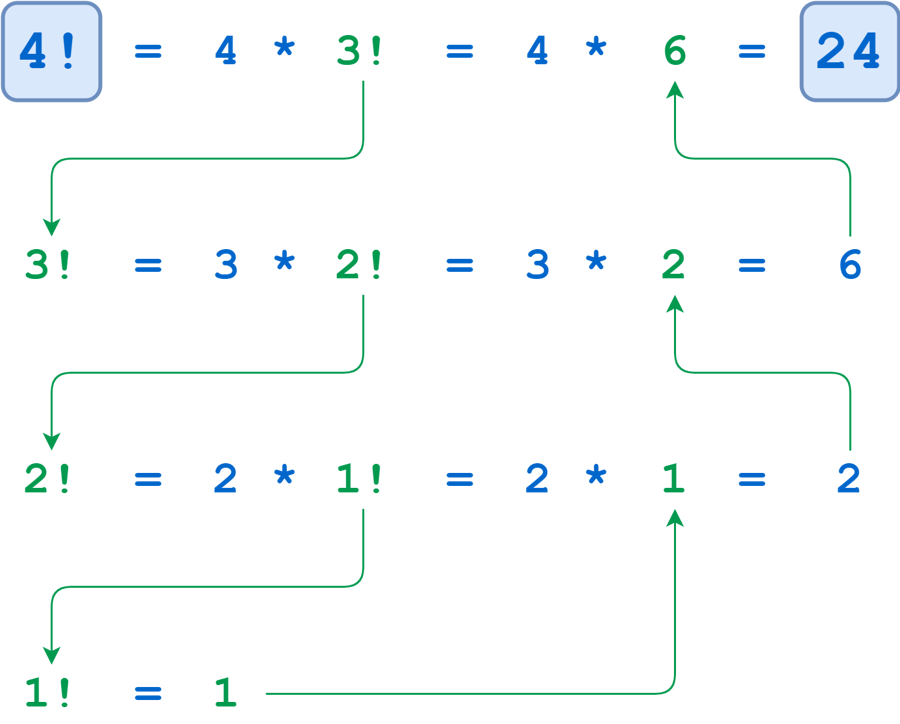
0>>> def factorial(n):
... return 1 if n <= 1 else n * factorial(n - 1)
...
>>> factorial(4)
24>>> def factorial(n):
... print(f"factorial() called with n = {n}")
... return_value = 1 if n <= 1 else n * factorial(n -1)
... print(f"-> factorial({n}) returns {return_value}")
... return return_value
...
>>> factorial(4)
factorial() called with n = 4
factorial() called with n = 3
factorial() called with n = 2
factorial() called with n = 1
-> factorial(1) returns 1
-> factorial(2) returns 2
-> factorial(3) returns 6
-> factorial(4) returns 24
24>>> def factorial(n):
... return_value = 1
... for i in range(2, n + 1):
... return_value *= i
... return return_value
...
>>> factorial(4)
24>>> from functools import reduce
>>> def factorial(n):
... return reduce(lambda x, y: x * y, range(1, n + 1) or [1])
...
>>> factorial(4)
24timeit(<command>, setup=<setup_string>, number=<iterations>)>>> from timeit import timeit
>>> timeit("print(string)", setup="string='foobar'", number=100)
foobar
foobar
foobar
.
. [100 repetitions]
.
foobar
0.03347089999988384>>> setup_string = """
... print("Recursive:")
... def factorial(n):
... return 1 if n <= 1 else n * factorial(n - 1)
... """
>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
Recursive:
4.957105500000125>>> setup_string = """
... print("Iterative:")
... def factorial(n):
... return_value = 1
... for i in range(2, n + 1):
... return_value *= i
... return return_value
... """
>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
Iterative:
3.733752099999947>>> setup_string = """
... from functools import reduce
... print("reduce():")
... def factorial(n):
... return reduce(lambda x, y: x * y, range(1, n + 1) or [1])
... """
>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
reduce():
8.101526299999932>>> from math import factorial
>>> factorial(4)
24>>> setup_string = "from math import factorial"
>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
0.3724050999999946names = [
"Adam",
[
"Bob",
[
"Chet",
"Cat",
],
"Barb",
"Bert"
],
"Alex",
[
"Bea",
"Bill"
],
"Ann"
]>>> len(names)
5>>> for index, item in enumerate(names):
... print(index, item)
...
0 Adam
1 ['Bob', ['Chet', 'Cat'], 'Barb', 'Bert']
2 Alex
3 ['Bea', 'Bill']
4 Ann>>> names
['Adam', ['Bob', ['Chet', 'Cat'], 'Barb', 'Bert'], 'Alex', ['Bea', 'Bill'], 'Ann']
>>> names[0]
'Adam'
>>> isinstance(names[0], list)
False
>>> names[1]
['Bob', ['Chet', 'Cat'], 'Barb', 'Bert']
>>> isinstance(names[1], list)
True
>>> names[1][1]
['Chet', 'Cat']
>>> isinstance(names[1][1], list)
True
>>> names[1][1][0]
'Chet'
>>> isinstance(names[1][1][0], list)
Falsedef count_leaf_items(item_list):
"""Recursively counts and returns the
number of leaf items in a (potentially
nested) list.
"""
count = 0
for item in item_list:
if isinstance(item, list):
count += count_leaf_items(item)
else:
count += 1
return count>>> count_leaf_items([1, 2, 3, 4])
4
>>> count_leaf_items([1, [2.1, 2.2], 3])
4
>>> count_leaf_items([])
0
>>> count_leaf_items(names)
10
>>> # Success! 1def count_leaf_items(item_list):
2 """Recursively counts and returns the
3 number of leaf items in a (potentially
4 nested) list.
5 """
6 print(f"List: {item_list}")
7 count = 0
8 for item in item_list:
9 if isinstance(item, list):
10 print("Encountered sublist")
11 count += count_leaf_items(item)
12 else:
13 print(f"Counted leaf item \"{item}\"")
14 count += 1
15
16 print(f"-> Returning count {count}")
17 return countdef fibonacciSimpleSum2(n):
# if 0 is less than n and n is less than 5 then we know we can return
# true because n will be 1-4 which can be created with 2 fib numbers
if 0 < n < 5:
return True
# first get fibonacci sequence up to n
seq = [0, 1]
# starting from 2 and ending at n
for i in range(2, n):
# add seq at i - 2 (0 to start) and seq at i - 1 (1 to start)
fib = seq[i - 2] + seq[i - 1]
# if n is greater than fib
if n >= fib:
# we can append fib to the sequence
seq.append(fib)
# if fib is greater than or equal to n we can stop
else:
break
print(seq)
# The check I googled
# for i, number in enumerate(seq[:-1]):
# paired = n - number
# if paired in seq[i + 1:]:
# return True
# check if any 2 of the numbers in seq add up to n
# My check
for i in range(len(seq) - 1): # O(n^2)
j = 0
while (seq[i] + seq[j]) != n:
if j == len(seq) - 1:
break
else:
j += 1
if seq[i] + seq[j] == n:
return True
return False
print(fibonacciSimpleSum2(5))def csSearchRotatedSortedArray(nums, target):
min = 0
max = len(nums) - 1
while not max < min:
guess = (max + min) // 2
# print(f'min: {nums[min]} max: {nums[max]} guess:{nums[guess]} target:'
# f' {target}')
# if the guess is the target we got it and return the guess
if nums[guess] == target:
# print('guessed the target')
return guess
# if min is less than or equal to the guess
elif nums[min] <= nums[guess]:
# print('min less than guess')
# if min is less than or equal to the target and less than the guess
if nums[min] <= target < nums[guess]:
# print('min less than or equal to target and less than guess')
# we can set max to the guess because nothing past the guess
# can be the target
max = guess
# else we can set min to guess + 1 because nothing before it
# can be the target
else:
# print('min is greater than target and greater than or equal '
# 'to guess')
min = guess + 1
# else if min is greater than the guess
else:
print('min is greater than or equal to guess')
# if max - 1 is greater than the target and greater than the guess
if nums[max - 1] >= target > nums[guess]:
# print('max - 1 greater than or equal to target and greater '
# 'than guess')
# we can set min to guess plus one because nothing before it
# can be the target
min = guess + 1
else:
# print('max -1 less than target and less than or equal to guess')
# else we set max equal to guess because nothing after it can
# be the target
max = guess
return -1C:\Lambda\CIRRICULUMN_NOTES\CS-python-notes_WEEKS\wk18\d4\homework\2021-09-09-14-03-46.png



def top_k_frequent(words, k):
"""
Input:
words -> List[str]
k -> int
Output:
List[str]
"""
frequency = {}
for word in words:
if word in frequency:
frequency[word] += 1
else:
frequency[word] = 1
sorted_data = sorted(frequency, key=lambda word: (-frequency[word], word))
return sorted_data[:k]
def helper(word):
return word
# Tests
print(top_k_frequent(["the", "sky", "is", "cloudy", "the", "the", "the", "cloudy", "is", "is"], 4))
print(top_k_frequent(["lambda", "school", "rules", "lambda", "school", "rocks"], 2))
# # Output
#
# ['the', 'is', 'cloudy', 'sky']
# ['lambda', 'school']
def djb2(key):
"""
DJB2 hash, 32-bit
"""
# Cast the key to a string and get bytes
str_key = str(key).encode()
# Start from an arbitrary large prime
hash_value = 5381
# Bit-shift and sum value for each character
for b in str_key:
hash_value = ((hash_value << 5) + hash_value) + b
hash_value &= 0xffffffff # DJB2 is a 32-bit hash, only keep 32 bits
return hash
def fnv1(key):
"""
FNV-1 hash, 64-bit
"""
# Cast the key to a string and get bytes
str_key = str(key).encode()
hash = 0x00000100000001B3 # FNV Prime
for b in str_key:
hash *= 0xcbf29ce484222325 # FNV Offset Basis
hash ^= b
hash &= 0xffffffffffffffff # 64-bit hash
return hash
"""# Load Factor
- if load factor is greater than 70% then double capacity of storage
- if load factor is less than 20% half capacity storage
"""
"""
1. Write the delete method with the assumption that linked list chaining was used for collision resolution.
2. Write the get method with the assumption that linked list chaining was used for collision resolution.
"""
class HashTableEntry:
"""
Linked List hash table key/value pair
"""
def __init__(self, key, value):
self.key = key
self.value = value
self.next = None
# Hash table can't have fewer than this many slots
# MIN_CAPACITY = 8
class HashTable:
"""
A hash table that with `capacity` buckets
that accepts string keys
Implement this.
"""
def __init__(self, capacity):
self.capacity = capacity # Number of buckets in the hash table
self.storage = [None] * capacity
self.item_count = 0
self.MIN_CAPACITY = 8
def get_num_slots(self):
"""
Return the length of the list you're using to hold the hash
table data. (Not the number of items stored in the hash table,
but the number of slots in the main list.)
"""
return len(self.storage)
def get_load_factor(self):
"""
Return the load factor for this hash table.
Implement this.
"""
return self.item_count / self.capacity
def djb2(self, key):
"""
DJB2 hash, 32-bit
Implement this, and/or FNV-1.
"""
# Cast the key to a string and get bytes
str_key = str(key).encode()
# Start from an arbitrary large prime
hash_value = 5381
# Bit-shift and sum value for each character
for b in str_key:
hash_value = ((hash_value << 5) + hash_value) + b
hash_value &= 0xffffffff # DJB2 is a 32-bit hash, only keep 32 bits
return hash_value
def hash_index(self, key):
"""
Take an arbitrary key and return a valid integer index
between within the storage capacity of the hash table.
"""
return self.djb2(key) % self.capacity
def put(self, key, value):
"""
Store the value with the given key.
Hash collisions should be handled with Linked List Chaining.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
while current_entry is not None and current_entry.key != key:
current_entry = current_entry.next
if current_entry is not None:
current_entry.value = value
else:
new_entry = HashTableEntry(key, value)
new_entry.next = self.storage[index]
self.storage[index] = new_entry
# increment the item count
self.item_count += 1
# resize based on load factor reaching higher than 70% (using a doubling strategy)
if self.get_load_factor() > 0.7:
self.resize(self.capacity * 2)
def delete(self, key):
"""
Remove the value stored with the given key.
Print a warning if the key is not found.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
last_entry = None
while current_entry is not None and current_entry.key != key:
last_entry = current_entry
current_entry = last_entry.next
if current_entry is None:
print("ERROR: Unable to remove the entry with a key of", key)
else:
if last_entry is None:
self.storage[index] = current_entry.next
else:
last_entry.next = current_entry.next
# decrement the item count
self.item_count -= 1
# TODO: resizing?
if self.get_load_factor() < 0.2:
if self.capacity > self.MIN_CAPACITY:
new_capacity = self.capacity // 2
if new_capacity < self.MIN_CAPACITY:
new_capacity = self.MIN_CAPACITY
self.resize(new_capacity)
def get(self, key):
"""
Retrieve the value stored with the given key.
Returns None if the key is not found.
Implement this.
"""
index = self.hash_index(key)
current_entry = self.storage[index]
# while the current entry exists
while current_entry is not None:
# check if the current entry key is the same as the passed in key
if current_entry.key == key:
# return the current entry value
return current_entry.value
# traverse to the next entry
current_entry = current_entry.next
return None
def resize(self, new_capacity): # O(n * k)
"""
Changes the capacity of the hash table and rehashes all of the key / value pairs
"""
# hold a ref to the old storage
old_storage = self.storage
# set the new capacity
self.capacity = new_capacity
# create the new storage
self.storage = [None] * self.capacity
# create a placeholder for the current entrys reference
current = None
# keep a copy of the original item count
old_count = self.item_count
# iterate over each bucket in the old storage
for bucket_item in old_storage:
# get the current entry
current = bucket_item
# while the current entry exists
while current:
# put the current entrys key value pair in to the new storage
self.put(current.key, current.value)
# traverse to the next entry
current = current.next
# restore the item count
self.item_count = old_count
if __name__ == "__main__":
ht = HashTable(8)
ht.put("line_1", "'Twas brillig, and the slithy toves")
ht.put("line_2", "Did gyre and gimble in the wabe:")
ht.put("line_3", "All mimsy were the borogoves,")
ht.put("line_4", "And the mome raths outgrabe.")
ht.put("line_5", '"Beware the Jabberwock, my son!')
ht.put("line_6", "The jaws that bite, the claws that catch!")
ht.put("line_7", "Beware the Jubjub bird, and shun")
ht.put("line_8", 'The frumious Bandersnatch!"')
ht.put("line_9", "He took his vorpal sword in hand;")
ht.put("line_10", "Long time the manxome foe he sought--")
ht.put("line_11", "So rested he by the Tumtum tree")
ht.put("line_12", "And stood awhile in thought.")
print("")
# Test storing beyond capacity
for i in range(1, 13):
print(ht.get(f"line_{i}"))
# Test resizing
old_capacity = ht.get_num_slots()
ht.resize(ht.capacity * 2)
new_capacity = ht.get_num_slots()
print(f"\nResized from {old_capacity} to {new_capacity}.\n")
# Test if data intact after resizing
for i in range(1, 13):
print(ht.get(f"line_{i}"))
print("")
"""# Demo"""
"""
You are given a non-empty list of words.
Write a function that returns the *k* most frequent elements.
The list that you return should be sorted by frequency from highest to lowest.
If two words have the same frequency, then the word with the lower alphabetical
order should come first.
Example 1:
```plaintext
Input:
words = ["lambda", "school", "rules", "lambda", "school", "rocks"]
k = 2
Output:
["lambda", "school"]
Explanation:
"lambda" and "school" are the two most frequent words.
```
Example 2:
```plaintext
Input:
words = ["the", "sky", "is", "cloudy", "the", "the", "the", "cloudy", "is", "is"]
k = 4
Output:
["the", "is", "cloudy", "sky"]
Explanation:
"the", "is", "cloudy", and "sky" are the four most frequent words. The words
are sorted from highest frequency to lowest.
```
Notes:
- `k` is always valid: `1 <= k <= number of unique elements.
- words in the input list only contain lowercase letters.
```
["the", "sky", "is", "cloudy", "the", "the", "the", "cloudy", "is", "is"]
freq = {"the": 4, "sky": 1, "is": 3, "cloudy": 2} sort this based on the values
res = ["the", "is", "cloudy", "sky"]
res[:k]
# get the freq of each word
# sort the dictionary besed on keys (maybe use a lambda)
# encapsulate this sorted dictionary inside another function to sort it alpha?
# then slice the results to constrain to k
"""
def top_k_frequent(words, k):
"""
Input:
words -> List[str]
k -> int
Output:
List[str]
"""
frequency = {}
for word in words:
if word in frequency:
frequency[word] += 1
else:
frequency[word] = 1
print(frequency)
# Tests
top_k_frequent(["the", "sky", "is", "cloudy", "the",
"the", "the", "cloudy", "is", "is"], 4)
# top_k_frequent(["lambda", "school", "rules", "lambda", "school", "rocks"], 2)