Write a Program to Find the Maximum Depth or Height of a Tree

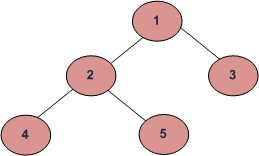
            maxDepth('1') = max(maxDepth('2'), maxDepth('3')) + 1
                               = 1 + 1
                                  /    \
                                /         \
                              /             \
                            /                 \
                          /                     \
               maxDepth('2') = 1                maxDepth('3') = 0
= max(maxDepth('4'), maxDepth('5')) + 1
= 1 + 0   = 1         
                   /    \
                 /        \
               /            \
             /                \
           /                    \
 maxDepth('4') = 0     maxDepth('5') = 0

# Python3 program to find the maximum depth of tree

# A binary tree node
class Node:

    # Constructor to create a new node
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

# Compute the "maxDepth" of a tree -- the number of nodes 
# along the longest path from the root node down to the 
# farthest leaf node
def maxDepth(node):
    if node is None:
        return 0 ; 

    else :

        # Compute the depth of each subtree
        lDepth = maxDepth(node.left)
        rDepth = maxDepth(node.right)

        # Use the larger one
        if (lDepth > rDepth):
            return lDepth+1
        else:
            return rDepth+1


# Driver program to test above function
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)


print ("Height of tree is %d" %(maxDepth(root)))

# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

<script>

// JavaScript program to find height of tree

// A binary tree node
class Node
{
    constructor(item)
    {
        this.data=item;
        this.left=this.right=null;
    }
}

    let root;
    
     /* Compute the "maxDepth" of a tree -- the number of
       nodes along the longest path from the root node
       down to the farthest leaf node.*/
    function maxDepth(node)
    {
        if (node == null)
            return 0;
        else
        {
            /* compute the depth of each subtree */
            let lDepth = maxDepth(node.left);
            let rDepth = maxDepth(node.right);
  
            /* use the larger one */
            if (lDepth > rDepth)
                return (lDepth + 1);
             else
                return (rDepth + 1);
        }
    }
    
    /* Driver program to test above functions */
    
        root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(4);
        root.left.right = new Node(5);
  
        document.write("Height of tree is : " +
                                      maxDepth(root));




// This code is contributed by rag2127

</script>

Height of tree is 2

#include <iostream>
#include <bits/stdc++.h>
using namespace std;

// A Tree node
struct Node
{
    int key;
    struct Node* left, *right;
};
  
// Utility function to create a new node
Node* newNode(int key)
{
    Node* temp = new Node;
    temp->key = key;
    temp->left = temp->right = NULL;
    return (temp);
}
  
/*Function to find the height(depth) of the tree*/
int height(struct Node* root){

    //Initialising a variable to count the 
      //height of tree
      int depth = 0;
  
    queue<Node*>q;
    
      //Pushing first level element along with NULL
      q.push(root);
    q.push(NULL);
    while(!q.empty()){
        Node* temp = q.front();
        q.pop();
      
          //When NULL encountered, increment the value
        if(temp == NULL){
            depth++;
        }
          
          //If NULL not encountered, keep moving
        if(temp != NULL){
            if(temp->left){
                  q.push(temp->left);
            }
              if(temp->right){
                q.push(temp->right);
            }
        }
      
          //If queue still have elements left,
          //push NULL again to the queue.
        else if(!q.empty()){
            q.push(NULL);
        }
    }
    return depth;
}

// Driver program
int main()
{
    // Let us create Binary Tree shown in above example
    Node *root  = newNode(1);
    root->left  = newNode(12);
    root->right = newNode(13);
  
    root->right->left   = newNode(14);
    root->right->right  = newNode(15);
  
    root->right->left->left   = newNode(21);
    root->right->left->right  = newNode(22);
    root->right->right->left  = newNode(23);
    root->right->right->right = newNode(24);
  
      cout<<"Height(Depth) of tree is: "<<height(root);
}