Calculating Big O

Order Of Growth

Notation

Big O Complexity Chart

Class Name Table

Simplifying Big O

Big O Python

# O(c) / o(1)
def constant_algo(items):
    result = items[0] * items[0] # O(1)
    print (result) # O(1)

    # O(2)
    # O(1)

constant_algo([4, 5, 6, 8])

# O(n)
def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

# What is the big O of this ??
# O(n) --> linear
def linear_algo_2(items):
    for item in items:
        print(item)
    for item in items:
        print(item)


linear_algo_2([4, 5, 6, 8])


# O(n^2)
def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

# chalenge. What is the complexity of this algorithm?

def complex_algo(items):

    for _ in range(5):
        print ("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

# itterative solution
def fact(n):
    product = 1
    for i in range(n): # O(n)
        product = product * (i + 1)
    return product

# recursive solution
def fact_r(n):
    if n == 0:
        return 1
    return n * fact_r(n - 1) # o(n)

JS

big ‘O’ notation

• Big O Notation is a tool for describing the efficiency of algorithms with respect to the size of the input arguments.

• Since we use mathematical functions in Big-O, there are a few big picture ideas that we’ll want to keep in mind:

• The function should be defined by the size of the input.

• Smaller Big O is better (lower time complexity)

• Big O is used to describe the worst case scenario.

• Big O is simplified to show only its most dominant mathematical term.

Simplifying Math Terms

• We can use the following rules to simplify the our Big O functions:

• Simplify Products : If the function is a product of many terms, we drop the terms that don't depend on n.

• Simplify Sums : If the function is a sum of many terms, we drop the non-dominant terms.

• n : size of the input

• T(f) : unsimplified math function

• O(f) : simplified math function.

Putting it all together

• First we apply the product rule to drop all constants.

• Then we apply the sum rule to select the single most dominant term.

Complexity Classes

Common Complexity Classes

There are 7 major classes in Time Complexity

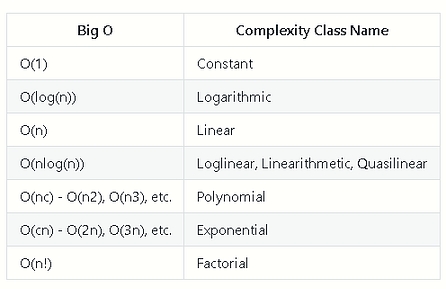
O(1) Constant

The algorithm takes roughly the same number of steps for any input size.

O(log(n)) Logarithmic

In most cases our hidden base of Logarithmic time is 2, log complexity algorithm’s will typically display ‘halving’ the size of the input (like binary search!)

O(n) Linear

Linear algorithm’s will access each item of the input “once”.

O(nlog(n)) Log Linear Time

Combination of linear and logarithmic behavior, we will see features from both classes.

Algorithm’s that are log-linear will use both recursion AND iteration.

O(nc) Polynomial

C is a fixed constant.

O(c^n) Exponential

C is now the number of recursive calls made in each stack frame.

Algorithm’s with exponential time are VERY SLOW.

Computing Big O

Brian "Beej Jorgensen" Hall edited this page on Nov 4, 2019 · 9 revisions

Goal: determine how runtime/number of operations scales up as the input scales up. How much longer does it take to run as the size of the data to process gets bigger?

Steps to compute Big O

• Things in sequence that aren't loops add together

• A single thing inside a loop gets multiplied by the loop

1. Go a line at a time, only looking at lines that are executable

2. Add all the things in sequence that you can first

3. Then multiply by the loops

4. Then repeat steps 2-3 as many times as you can

5. Then keep the dominant term from the resulting sum(s)

6. Then drop constants

Hints

• If you have something that's O(number_of_elements_in_the_data), we use n as shorthand for number_of_elements_in_the_data, so O(n).

• Individual statements tend to be O(1).

• Loop statements tend to be O(how-many-times-they-loop).

• Anything that doubles the runtime each step is O(2^n) (e.g. naive Fibonacci).

• Anything that triples the runtime each step is O(3^n).

• Anything that halves the runtime each step is O(log n) (e.g. binary search).

• By dominant term we mean, "thing which is largest given some large value of n, like 10000". O(n) dominates O(1). O(n^2) dominates O(n) and O(1).

• Loops that iterate over entire lists are O(n), where n is the size of the list.

• But loops that binary search over a list are O(log n)!

Recursion

• Recursive functions are like loops, where the body of the function is the body of the loop.

• You need to figure out how many times the function will call itself, and that's the Big O that you need to multiply against the Big O of the function body.

• Keep in mind that recursion comes with an inherent memory cost that loops don't incur, since each recursive call adds an additional execution frame to the stack; in other words, calling a function is not free!

Gotchas

• Built in functions might incur significant Big O without you noticing. Python's list .copy() might seem like just a simple O(1) line, but it's O(n) under the hood.

• Beware of loops that modify their index in weird ways.

Example

Label all statements by their time complexities. Individual statements get their Big O, while loops get the number of times they loop.

def foo(n):
    a = 10                # O(1)
    b = 20                # O(1)

    for i in range(n):    # O(n)
        a += b               # O(1)
        b += 1               # O(1)

    for j in range(n**2): # O(n^2)
        a -= 2               # O(1)
        print(a)             # O(1)

        for k in range(n/2): # O(n/2)
            print(k)             # O(1)

    return a + b          # O(1)

Now we'll replace the lines of code with their Big O for brevity:

def foo(n):
    # O(1)
    # O(1)

    # O(n)
        # O(1)
        # O(1)

    # O(n^2)
        # O(1)
        # O(1)

        # O(n/2)
            # O(1)

    # O(1)

Try to add things in sequence, but remember that loops interrupt sequences!

def foo(n):
    # O(2)    -- was O(1) + O(1)

    # O(n)
        # O(2)    -- was O(1) + O(1)

    # O(n^2)
        # O(2)    -- was O(1) + O(1)

        # O(n/2)
            # O(1)

    # O(1)

Now we see if we can multiply any loops by their bodies.

def foo(n):
    # O(2)

    # O(2 * n)    -- had body O(2)

    # O(n^2)      -- can't do this one yet--body has more than one item
        # O(2)

        # O(1 * n/2)    -- had body O(1)

    # O(1)

Let's try to add any sequences again.

def foo(n):
    # O(2 + 2 * n)

    # O(n^2)
        # O(2 + 1 * n/2)

    # O(1)

Now let's try multiplying loops again

def foo(n):
    # O(2 + 2 * n)

    # O(n^2 * (2 + 1 * n/2))

    # O(1)

Add add sequences again:

def foo(n):
    # O((2 + 2 * n) + (n^2 * (2 + 1 * n/2)) + 1)

Now we're down to one line. That's the time complexity, but we need to reduce it.

Break out your algebra.

(2 + 2 * n) + (n^2 * (2 + 1 * n/2)) + 1   From the Big O, above
2 + 2 * n + n^2 * (2 + 1 * n/2) + 1       Lose unnecessary parens
3 + 2 * n + n^2 * (2 + 1 * n/2)           Add some like terms
3 + 2 * n + n^2 * (2 + n/2)               1* is does nothing
3 + 2 * n + 2 * n^2 + n/2 * n^2           Distribute n^2
3 + 2 * n + 2 * n^2 + 1/2 * n * n^2       Note the n/2 is 1/2*n
3 + 2 * n + 2 * n^2 + 1/2 * n^3           n * n^2 = n^3
(3) + (2 * n) + (2 * n^2) + (1/2 * n^3)   Choose the most dominant from the sum
1/2 * n^3                                 1/2 * n^3 grows fastest, is dominant
n^3                                       Drop the constant

O(n^3) is the time complexity of this function.

With practice, you can do this in your head. Looking back, the nested loop must have been where the function spent the most of its time; an experienced dev would see that and just quickly compute the Big O for that function from that nested loop alone.

Example with two variables

def foo(m, n):
    for i in range(m * n):
        print(i)

When you have two inputs like this, there's no way to reduce it farther than O(m*n) (or O(n*m), same thing). That's the answer.

Sometimes when m and n tend to be roughly similar, developers will casually say this is O(n^2), but it's really O(m*n).

Example with lists

def foo(x):  # x is a list
    for i in x:    # O(n)
        print(i)       # O(1)

In this example, we're not explicitly passing in an n parameter, but rather a list.

The list has a number of elements in it, and we refer to this number as n by default.

The for loop is therefore O(n), because it will iterate one time for each element in the list.

Another example:

def foo(x, y):  # x and y are lists
    for i in x:    # O(n)
        for j in y:    # O(m)
            print(i, j)    # O(1)

Here we've used n to represent the number of elements in list x, and m to represent the number in list y.

We can use our simplification rules and see that the entire function is O(n*m*1), or O(n*m). (Or O(n^2) if we're speaking informally, and assuming that n and m are very similar.)

Example with trivial recursion

def foo(x):   # x is a list
    if len(x) == 0:
        return

    print(x[0])
    foo(x[1:])

The above function prints out every element in a list. But it's trickier to see what the Big O is. Our normal rules don't work entirely well.

The secret is that recursive functions are like loops on steroids. So you know it's similar to a loop in that it's going to perform a number of operations. But how many? n? n^2? We have to figure it out.

In the above example, each call to foo() results in one more call to foo(). (Because we look in the body of the function and we see it only calls itself once.) And it's going to keep calling itself a number of times. How many times will foo() call itself?

Here, if we declare that n is the number of elements in list x, foo() calls itself n times, once for each element in x.

So the recursion itself, acting like a loop, is O(n).

We still have to look at the things inside foo() to see what else is going on. The body of foo() becomes like the body of the loop.

But it looks like in there we only have a couple O(1) things, so the whole thing becomes O(n * (1 + 1)), aka O(2n) AKA O(n). Final answer.

Example with Fibonacci

def fib(n):   # Give me the nth Fibonacci number
    if n < 2:
        return n

    return fib(n-2) + fib(n-1)  # Calls itself twice per call!

Again, think loop on steroids. fib() calls itself... but it calls itself two times per call. ...ish.

We call it 1 time, it calls itself 2 times. Those 2 times call it 4 times, which call it 8 times, which call it 16 times, etc. If you recognize those numbers, you'll know those are powers of 2. 2^0=1, 2^1=2, 2^2=4, 2^3=8, and all the way up to 2^n.

This is an O(2^n) recursive call. (With an O(1) body.)

Sure, fib(n-2) only calls it 1/2 * n times, but we chuck that constant for Big O.

And the base case won't necessarily let n get all the way down to zero, but those are just some -1s or -2s, and those terms aren't dominant in Big O.